Geschreven door: Thomas van Osch
De aerodynamica van een F1-auto, de aandelenkoers van Tesla, de verspreiding van ziekten en de simulatie van zwarte gaten – wat hebben deze concepten met elkaar gemeen?
Dit zijn slechts enkele voorbeelden waarbij (partiële) differentiaalvergelijkingen kunnen helpen bij het modelleren en begrijpen van verschijnselen die anders moeilijk of zelfs onmogelijk te verklaren zouden zijn. In plaats daarvan geven partiële differentiaalvergelijkingen een breed scala aan domeinen een wiskundig kader om zeer complexe systemen te beschrijven. Zoals je je kunt voorstellen, is het oplossen van deze krachtige vergelijkingen geen triviale taak. Dus hoe pakken we dit aan en waar komt HPC om de hoek kijken?
Te gewoontjes?
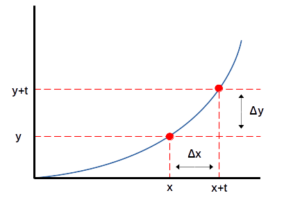
Laten we ons eerst vertrouwd maken met differentiaalvergelijkingen. De term differentieel beschrijft hoe een grootheidverandert ten opzichte van een andere grootheid. Zie de grafiek hieronder met twee assen. Op de horizontale as meten we een hoeveelheid met x tegen een hoeveelheid y op de verticale as. De relatie tussen deze twee grootheden wordt weergegeven door de blauwe lijn als een functie. Stel nu dat we de snelheid(y-as) van een auto in de tijd(x-as) willen modelleren.
Aan de blauwe lijn kunnen we zien dat de auto eerst zijn motor moet starten en een goede acceleratie moet bereiken voordat de snelheid snel omhoog gaat. Door afgeleiden te gebruiken, kunnen we binnen een tijdspanne Δx tussen x en x + t, zeg tussen 1 minuut en 2 minuten, hoeveel de auto is versneld in termen van Δy. Of technischer, de afgeleide beschrijft de snelheid waarmee de snelheid verandert. Dit is erg
nuttig omdat het inzicht geeft in hoe verschillende fasen van de acceleratie van de auto zich gedragen. Van hieruit kunnen we zien waar de acceleratie kan worden verbeterd en de snelheid vergelijken met andere auto’s.
Een gewone differentiaalvergelijking
Een differentiaalvergelijking oplossen betekent de functie vinden die aan de vergelijking voldoet. In ons voorbeeld van een auto kan de enkele variabele snelheid worden beschreven in een enkele functie om de snelheid in de tijd te modelleren. Vergelijkingen waarbij een individuele variabele verandert ten opzichte van een enkele andere variabele noemen we een gewoon differentiaalvergelijking. In de echte wereld is de functie niet altijd gewoon en beïnvloeden meerdere variabelen wat we willen meten. Dus hoe pakken we dit aan?
Hoe te begrijpen: een voorbeeld van partiële differentialen in actie
Stel je voor dat je de beweging van water in een rivier probeert te voorspellen. De snelheid en richting van de stroming is op elk punt in de rivier meetbaar. We willen echter weten hoe de stroom in de toekomst (tijd) en op verschillende locaties (ruimte) zal veranderen. Een andere moeilijkheid is dat we rekening moeten houden met verschillende factoren zoals de stroomsnelheid van het water, de vorm van de rivierbedding, de wrijving van de grond, enz. Al deze variabelen beïnvloeden de stroom. Met partiële differentialen kunnen we de functie van de waterstroom en de invloed van de afzonderlijke factoren afleiden. PDE’s geven ons dan een raamwerk om de relatie tussen individuele variabelen tot een bepaalde grootheid in tijd en ruimte te modelleren.
In complexe fysische systemen met veel op elkaar inwerkende variabelen en factoren is de wiskundige functie om het fysische fenomeen te modelleren vaak moeilijk nauwkeurig op te lossen. Zelfs dan zijn deze oplossingen mogelijk niet stabiel of reproduceerbaar. Meestal moeten we PDE’s oplossen door kleine stapjes te nemen om steeds dichter bij de echte oplossing te komen. Zelfs elk van deze kleine stappen brengt een grote hoeveelheid berekeningen met zich mee. Hier komen computers om de hoek kijken, zoals we hieronder zullen zien.
Hoewel partiële differentiaalvergelijkingen ingewikkeld klinken, zijn ze in wezen gewoon een hulpmiddel dat wetenschappers gebruiken om te begrijpen hoe dingen bewegen en veranderen in de wereld om ons heen.
Partiële differentiaalvergelijkingen (PDE’s) schalen
Berekeningen om een oplossing voor PDE’s af te leiden zijn kostbaar en tijdrovend. In de praktijk gaat het bij PDE’s vaak om het uitvoeren van bewerkingen op grote matrices waarin krachtige computers uitblinken. Door de matrices te ontbinden, grootschalige parallelle verwerking mogelijk te maken en HPC-specifieke numerieke methoden te ontwikkelen, wordt het nauwkeuriger benaderen van deze PDE’s haalbaarder. Bovendien bieden de toepassing van deep learning op partiële differentiaalvergelijkingen en de steeds prominentere aanwezigheid van GPU-infrastructuur in rekenclusters nog meer mogelijkheden.
Terwijl onderzoekers doorgaan met het ontwikkelen van nieuwe technologieën en numerieke methoden om partiële differentiaalvergelijkingen beter te benaderen, terwijl de gemeenschap steeds grotere datacenters blijft bouwen, heeft de combinatie van PDE’s en HPC ons al geleid en zal ons blijven leiden naar belangrijke doorbraken in ons begrip van natuurkunde, economie en sociale wetenschappen – om maar een paar van de enorme landschappen te noemen waar PDE’s een verschil kunnen maken. Wie weet wat PDE’s ons zullen vertellen over de oorsprong en toekomst van ons universum?
SURF
Vanuit het perspectief van SURF, een nationaal competentiecentrum, zien we een toename in adviesaanvragen en geavanceerd onderzoek naar partiële differentiaalvergelijkingen vanuit verschillende domeinen. In het bijzonder wordt deep learning nu gecombineerd met PDE’s om tot nauwkeurigere oplossingen en voorspellingen te komen voor weersvoorspellingen, moleculaire structurering en meer. Het machine learning team binnen SURF ontwikkelt ook generieke neurale PDE solvers om het concept te begrijpen en biedt niet alleen HPC-infrastructuur, maar ook technische en wetenschappelijke inzichten in het verder verbeteren van deze modellen.

